“สัญญาณรบกวน(Noise)จำนวนมากสามารถครอบงำสัญญาณภาพ(Signal)ได้”
ในทางสถิติ t-test เป็นการทดสอบสมมติฐานประเภทหนึ่งที่ให้คุณทำการเปรียบเทียบค่ากลาง พวกเขาเรียกว่า t-test เพราะว่าในการทดสอบ t-test แต่ละครั้งคือจะทำให้ข้อมูลตัวอย่างของคุณลดลงเหลือเพียงตัวเลขเดียวคิอค่า t-value หากคุณเข้าใจว่าการทดสอบ t-test คำนวณค่า t-value อย่างไรคุณก็สามารถทำความเข้าใจว่าการทดสอบเหล่านี้ทำงานอย่างไร
ในโพสต์ชุดนี้ฉันมุ่งเน้นไปที่แนวคิดมากกว่าสมการเพื่อแสดงว่าการทดสอบ t-test ทำงานอย่างไร แต่อย่างไรก็ตามโพสต์นี้จะแสดงสมการง่ายๆสองสมการที่ฉันจะใช้ดำเนินการเปรียบเทียบอัตราส่วนสัญญาณภาพต่อสัญญาณรบกวน(signal-to-noise ratio)
ซอฟต์แวร์ Minitab มีการทดสอบ 1-sample t-test, paired t-test, และ 2-sample t-test มาดูกันว่าการทดสอบ t-test แต่ละแบบเหล่านี้คำนวณข้อมูลตัวอย่างลงเหลือแค่ค่า t-value อย่างไร
การทดสอบ t-test คำนวณค่า t-value อย่างไร
การทำความเข้าใจกระบวนการนี้มีความสำคัญต่อการทำความเข้าใจว่าการทดสอบ t-test ทำงานอย่างไร ฉันจะแสดงสูตรให้คุณเห็นก่อน จากนั้นฉันจะอธิบายวิธีการทำงาน
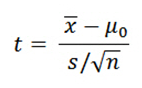
โปรดสังเกตว่าสูตรเป็นอัตราส่วน เทียบง่ายๆก็คือค่า t-value คืออัตราสัญญาณภาพต่อสัญญาณรบกวน(signal-to-noise ratio)
สัญญาณภาพ(Signal) หรือที่เรียกว่าขนาดผลกระทบ (effect size)
ตัวเศษคือสัญญาณภาพ(Signal) คุณเพียงแค่หาค่าเฉลี่ยข้อมูลตัวอย่างแล้วลบด้วยค่าสมมุติฐานหลัก ถ้าค่าเฉลี่ยข้อมูลตัวอย่างของคุณคือ 10 และสมมติฐานหลักของคุณคือ 6 ความแตกต่างหรือสัญญาณภาพคือ 4
ถ้าไม่มีความแตกต่างระหว่างค่าเฉลี่ยข้อมูลตัวอย่างกับค่าสมมติฐานหลัก สัญญาณภาพคือค่าเศษจะเท่าๆกับค่าอัตราส่วนที่ได้ ตัวอย่างเช่นถ้าค่าเฉลี่ยข้อมูลตัวอย่างของคุณคือ 6 และค่าสมมติฐานหลักคือ 6 ดังนั้นความแตกต่างจะเป็นศูนย์
เมื่อความแตกต่างระหว่างค่าเฉลี่ยข้อมูลตัวอย่างและค่าเฉลี่ยของสมมติฐานหลักเพิ่มขึ้นในทิศทางบวกหรือลบทั้งคู่ แสดงว่าความแรงของสัญญาณภาพเพิ่มขึ้น
สัญญาณรบกวน (Noise)
ตัวส่วนคือสัญญาณรบกวน(Noise) สมการในตัวส่วนเป็นการวัดความแปรปรวนที่เรียกว่าข้อผิดพลาดมาตรฐานของค่าเฉลี่ย(standard error of mean) สถิตินี้ระบุว่ากลุ่มตัวอย่างของคุณประเมินค่าเฉลี่ยของประชากรได้แม่นยำเพียงใด ตัวเลขที่มากขึ้นแสดงว่าค่าประมาณตัวอย่างของคุณแม่นยำน้อยกว่าเนื่องจากมีข้อผิดพลาดแบบสุ่มมากกว่า
ข้อผิดพลาดแบบสุ่มนี้คือ “สัญญาณรบกวน(noise)” เมื่อมีสัญญาณรบกวนมากขึ้น คุณคาดว่าจะได้เห็นความแตกต่างระหว่างค่าเฉลี่ยตัวอย่างและค่าสมมติฐานหลักที่มากขึ้นแม้ว่าสมมติฐานหลักจะเป็นจริงก็ตาม เรานำปัจจัยสัญญาณรบกวนไว้ในตัวส่วนเพราะว่าเราต้องหาว่าสัญญาณภาพชัดเจนโดดเด่นพอหรือไม่
สัญญาณภาพต่อสัญญาณรบกวน(Signal-to-Noise ratio)
ทั้งค่าสัญญาณภาพและสัญญาณรบกวนของข้อมูลของคุณอยู่ในหน่วยเดียวกัน ถ้าสัญญาณภาพของคุณคือ 6 และสัญญาณรบกวนคือ 2 ค่า t-value ของคุณคือ 3 ,ค่า t-value นี้บ่งชี้ว่าความแตกต่างมีขนาด 3 เท่าของข้อผิดพลาดมาตรฐาน อย่างไรก็ตามหากความแตกต่างที่มีขนาดเท่ากัน แต่ถ้าข้อมูลของคุณมีความแปรปรวนมากขึ้น (6), ค่า t-value ของคุณเหลือเพียงแค่ 1 สัญญาณภาพจะอยู่ในระดับเดียวกับสัญญาณรบกวน
ด้วยวิธีนี้ค่า t-value จะช่วยให้คุณแยกได้ว่าสัญญาณภาพของคุณแตกต่างจากสัญญาณรบกวนเพียงใด แสดงความสัมพันธ์ สัญญาณภาพที่ค่อนข้างแรงในขณะที่ระดับสัญญาณกวนต่ำจะทำให้เกิดค่า t-value ที่มากขึ้น หากสัญญาณภาพไม่ชัดเจนโดดเด่นจากสัญญาณรบกวนอาจเป็นไปได้ว่าความแตกต่างที่สังเกตได้ระหว่างค่าประมาณจากข้อมูลตัวอย่างกับค่าสมมติฐานหลักเกิดจากข้อผิดพลาดแบบสุ่มในตัวอย่างแทนที่จะเป็นความแตกต่างที่แท้จริงในระดับประชากร
Paired t-test ก็คือการทดสอบแบบ 1-sample t-test
หลายคนสับสนว่าเมื่อไหร่ควรใช้ Paired t-test และมันทำงานอย่างไร ฉันจะบอกคุณเกี่ยวกับความลับเล็กๆน้อยๆ, แท้ที่จริงแล้ว Paired t-test และ 1-sample t-test เหมือนกันแต่เรียกคนละชื่อ ดังที่เราเห็นข้างต้น 1 sample t-test เปรียบเทียบค่าเฉลี่ยตัวอย่างหนึ่งค่ากับค่าสมมุติฐานหลัก การทดสอบ Paired test จะคำนวณความแตกต่างระหว่างการสังเกตแบบจับคู่ (เช่นก่อนและหลัง) จากนั้นทำการทดสอบ 1 sample t-test กับค่าความแตกต่างนั้น
คุณสามารถทดสอบสิ่งนี้ด้วยชุดข้อมูลนี้เพื่อดูว่าผลลัพธ์ทั้งหมดเหมือนกันเพียงใดรวมถึงค่าความแตกต่างเฉลี่ย, ค่า t-value, ค่า p-value และช่วงความเชื่อมั่นของความแตกต่าง
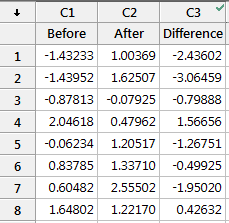


ให้เข้าใจว่า Paired t-test เป็นเพียงแค่ทำการทดสอบ 1 sample t-test ของความแตกต่างที่จับคู่กัน สามารถช่วยให้คุณเข้าใจวิธีการทำงานของ Paired t-test และควรใช้เมื่อใด คุณเพียงแค่ต้องหาว่าการคำนวณความแตกต่างระหว่างการสังเกตแต่ละคู่เหมาะสมหรือไม่
ตัวอย่างเช่น สมมติว่า “ก่อน” และ “หลัง” แสดงถึงคะแนนการทดสอบ คะแนนก่อนและหลังในแต่ละแถวของเวิร์คชีทตัวอย่างเป็นตัวแทนของรายวิชาเดียวกัน และสามารถมีการสลับสับลำดับคะแนนระหว่างกันได้หรือไม่ (สลับลำดับไม่ได้) การคำนวณความแตกต่างระหว่างคะแนนในลักษณะจับคู่นี้ก็สมเหตุสมผล อย่างไรก็ตามหากคะแนนในแต่ละแถวเป็นคะแนนสำหรับวิชาที่แตกต่างกันการคำนวณความแตกต่างก็ไม่อาจสมเหตุสมผล ในกรณีนี้คุณต้องไปใช้การทดสอบแบบอื่น เช่น 2 sample t-test ซึ่งจะคุยกันต่อไป
การใช้ Paired t-test จะช่วยให้คุณประหยัดขั้นตอนในการคำนวณความแตกต่างก่อนทำการทดสอบ t-test แต่คุณต้องแน่ใจว่าความแตกต่างที่จับคู่นั้นสมเหตุสมผล!
เมื่อใดก็ตามเหมาะสมที่จะใช้ การทดสอบแบบ Paired t-test จะมีประสิทธิภาพมากกว่า 2 sample t-test สำหรับข้อมูลเพิ่มเติมเรื่องการทดสอบแบบ Paired t-test ไปที่หัวเรื่อง “Overview for paired t”
การทดสอบ 2 sample t-test คำนวณค่า t-value อย่างไร
การทดสอบแบบ 2 sample t-test นำข้อมูลตัวอย่างมากจากสองกลุ่มและทำการลดให้เหลือเพียงค่า t-value เพียงตัวเดียว กระบวนการคล้ายๆกับ 1 sample t-test และคุณยังคงใช้หลักการของสัญญาภาพต่อสัญญาณรบกวนได้เหมือนเดิมแต่ไม่เหมือนกับ Paired t-test โดย 2 sample t-test ข้อมูลตัวอย่างจากสองกลุ่มต้องเป็นอิสระต่อกัน
ดูสูตรคำนวณข้างล่างและเรามาคุยกัน
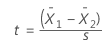
สำหรับการทดสอบ 2 sample t-test ตัวเศษจะเป็นสัญญาณภาพ(signal) เช่นเดิมซึ่งเป็นค่าความแตกต่างระหว่างค่าเฉลี่ยของทั้งสองตัวอย่าง ตัวอย่างเช่นถ้าค่าเฉลี่ยของกลุ่ม 1 คือ 10 และค่าเฉลี่ยของกลุ่ม 2 คือ 4 ผลต่างคือ 6
ค่าเริ่มต้นสมมติฐานหลักสำหรับการทดสอบ 2 sample t-test คือทั้งสองกลุ่มมีค่าเท่ากัน คุณจะเห็นในสมการว่าเมื่อทั้งสองกลุ่มเท่ากันผลต่าง (และค่าอัตราส่วน) จะเท่ากับศูนย์ด้วย เมื่อความแตกต่างระหว่างทั้งสองกลุ่มเพิ่มขึ้นในทิศทางบวกหรือลบสัญญาณภาพก็จะชัดเจนขึ้น
ในการทดสอบ 2 sample t-test ตัวส่วนยังคงเป็นสัญญาณรบกวน(noise) แต่ Minitab สามารถใช้ค่าที่ต่างกันสองค่าได้ คุณสามารถสมมติได้ว่าความแปรปรวนในทั้งสองกลุ่มเท่ากันหรือไม่เท่ากันและ Minitab ใช้ค่าประมาณของความแปรปรวนที่เราตั้งสมมติฐานไว้ ซึ่งไม่ว่าจะด้วยวิธีใดหลักการก็ยังคงเหมือนเดิม: คุณกำลังเปรียบเทียบสัญญาณภาพของคุณกับสัญญาณรบกวนเพื่อดูว่าสัญญาณนั้นชัดเจนโดดเด่นมากแค่ไหน
เช่นเดียวกับการทดสอบ 1 sample t-test ,ค่าความแตกต่างที่กำหนดในตัวเศษเมื่อคุณเพิ่มค่าสัญญาณรบกวนในตัวส่วนค่า t-value จะลดลง ในการพิจารณาว่ากลุ่มต่างกันหรือไม่คุณต้องมีค่า t-value ที่มีขนาดใหญ่
ค่า t-value หมายถึงอะไร?
การทดสอบ t-test แต่ละประเภทใช้ขั้นตอนในการลดข้อมูลตัวอย่างทั้งหมดของคุณให้เหลือค่าเดียวคือค่า t-value การคำนวณจะเปรียบเทียบค่าเฉลี่ยตัวอย่างของคุณกับสมมติฐานหลักและรวมถึงพิจารณาทั้งขนาดตัวอย่างและความแปรปรวนในข้อมูล ค่า t-value เป็น 0 หมายถึงว่าค่าประมาณของตัวอย่างเท่ากับสมมติฐานหลักทุกประการ ในทางสถิติเราเรียกความแตกต่างระหว่างค่าประมาณตัวอย่างและสมมติฐานหลักว่าขนาดผลกระทบ เมื่อความแตกต่างนี้เพิ่มขึ้นค่าสัมบูรณ์(absolute)ของค่า t-value จะเพิ่มขึ้น
ทั้งหมดนี้เมื่อเข้าใจแล้ว ว่าแต่ค่า t-value หมายความถึงอะไร? สมมติว่าได้ค่าเท่ากับ 2 จริงๆแล้วหมายถึงอะไร จากการอภิปรายข้างต้นเราทราบว่าค่า t-value เท่ากับ 2 หมายความว่าความแตกต่างที่สังเกตได้มีขนาดเป็นสองเท่าของความแปรปรวนในข้อมูลของคุณ อย่างไรก็ตามเราใช้การทดสอบค่า t-test เพื่อประเมินสมมติฐานมากกว่าการหาอัตราส่วนสัญญาณภาพต่อสัญญาณรบกวน เราต้องการหาว่าขนาดผลกระทบมีนัยสำคัญทางสถิติหรือไม่
หากต้องการรู้ว่าเราได้ค่า t-value มาได้อย่างไรไปจนถึงการประเมินสมมติฐานและการกำหนดนัยสำคัญทางสถิติ อ่านโพสต์เรื่อง : “ทำความเข้าใจการทดสอบสมมติฐาน t-Tests, ค่า t-values และการแจกแจงแบบ t-distributions”
บทความต้นฉบับ : Understanding t-Tests: 1-sample, 2-sample, and Paired t-Tests
ต้นฉบับนำมาจาก Minitab blog , แปลและเรียบเรียงโดยชลทิชา จํารัสพร
บริหารจัดการ SCM Blog โดยชลทิชา จำรัสพร, บริษัท โซลูชั่น เซ็นเตอร์ จํากัด ตัวแทน Minitab ในประเทศไทย

เพิ่มเติมเกี่ยวกับบริษัท Minitab
Minitab ช่วยให้บริษัทและองค์กรต่างๆ สามารถมองเห็นแนวโน้มของข้อมูล, แก้ปัญหาและค้นพบประเด็นสำคัญจากข้อมูลเชิงลึก โดยนำเสนอชุดโซลูชั่นที่ครอบคลุมทุกด้านและดีที่สุดสำหรับซอฟต์แวร์ในระดับเดียวกัน ที่ใช้สำหรับการวิเคราะห์ข้อมูลและการปรับปรุงกระบวนการ
ด้วยวิธีการที่เป็นเอกลักษณ์ และการนำเสนอซอฟต์แวร์และบริการแบบองค์รวม Minitab ช่วยให้องค์กรเข้าถึงกระบวนการตัดสินใจในส่วนที่ช่วยผลักดันให้เกิดความเป็นเลิศทางธุรกิจได้ดีขึ้น ความง่ายในการใช้งานที่โดดเด่นกว่าใครมีส่วนช่วยให้ Minitab สามารถทำให้การเข้าถึงข้อมูลเชิงลึกเป็นเรื่องที่ง่าย ทีมงานของ Minitab ซึ่งประกอบด้วยผู้เชี่ยวชาญทางด้านการวิเคราะห์ข้อมูลที่ได้ผ่านการอบรมมาเป็นอย่างเข้มงวด จะช่วยให้ผู้ใช้งานมั่นใจว่าจะได้รับประโยชน์สูงสุดจากการใช้งานวิเคราะห์ข้อมูลและพร้อมที่จะให้คำปรึกษาตลอดเวลาที่ใช้งานเพื่อนำไปสู่การตัดสินใจที่ดีขึ้น รวดเร็ว และแม่นยำ
เป็นเวลากว่า 50 ปีที่ Minitab ได้ช่วยองค์การต่าง ๆ เพิ่มรายได้ ควบคุมและลดต้นทุน เพิ่มคุณภาพ เสริมสร้างความพึงพอใจของลูกค้า และเพิ่มประสิทธิภาพ ธุรกิจและองค์นับหมื่นทั่วโลกใช้ Minitab Statistical Software®, Companion by Minitab®, Minitab Workspace®, Salford Predictive Modeler® and Quality Trainer® เป็นเครื่องมือช่วยในการค้นพบและปรับปรุงความบกพร่องในกระบวนการ

