กราฟ Probability Plot ไม่ได้มีเพียงค่า p-value เท่านั้น แต่รูปแบบของกราฟโดยรวมยังให้ข้อมูลที่มีประโยชน์อีกด้วย ซึ่งกราฟ Probability Plot เป็นเครื่องมือที่มีประสิทธิภาพในการทำความเข้าใจข้อมูลของคุณได้ดียิ่งขึ้น
ในบทความนี้ ฉันตั้งใจที่จะนำเสนอหลักการสำคัญของกราฟ Probability Plot และเน้นไปที่การตีความจากรูปแบบของกราฟ โดยใช้ตัวอย่างจากข้อมูลจริง
ในกราฟ Probability Plot การแจกแจงความหนาแน่นของความน่าจะเป็นของข้อมูล (Density Distribution) จะถูกแปลงเป็นกราฟเชิงเส้นตรง การจะทำเช่นนี้ได้ จะต้องใช้ฟังก์ชั่นความน่าจะเป็นสะสม (Cumulative Density Function หรือ CDF ซึ่งเป็นการนำค่าความน่าจะเป็นทั้งหมดที่มีค่าน้อยกว่าเกณฑ์ที่กำหนดมารวมกัน) ตามรูปด้านล่าง โดย CDF ของการแจกแจงแบบปกติ (Normal Distribution) จะมีลักษณะเป็นเส้นโค้งรูปตัว S และเพื่อแปลงเส้นโค้งรูปตัว S นี้ให้เป็นเส้นตรง จำเป็นต้องใช้สเกลพิเศษ Gausso-arithmetic (nonlinear) สำหรับสเกลแกน Y แนวตั้ง
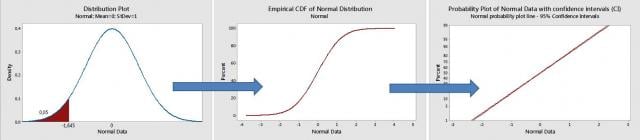
หากค่า p-value มีค่าต่ำ แสดงว่า ปฏิเสธสมมติฐานที่ว่าข้อมูลมาจากการแจกแจงปกติ แต่ว่าฉันต้องการเน้นไปที่การวิเคราะห์รูปแบบของกราฟ Probability Plot โดยพิจารณาจากลักษณะที่ปรากฏของข้อมูล เพื่อประเมินว่า จุดต่างๆ อยู่ใกล้เส้นตรงแค่ไหน โดยมักใช้กับการทดสอบ “Fat Pencil” คือ ให้จินตนาการว่า เรามีดินสอที่มีเส้นหนาใหญ่ แล้วลากเส้นลงบนกราฟ ถ้าจุดข้อมูลทั้งหมดเรียงตัวอยู่ภายในเส้นดินสอที่มีความหนานี้ แสดงว่า เป็นไปตามสมมติฐานของการแจกแจงของข้อมูล (ในกรณีนี้คือ การแจกแจงปกติ)
การใช้กราฟ Probability Plot เพื่อระบุค่าผิดปกติ (Outliers) หรือระบุผลกระทบอย่างมีนัยสำคัญ
กราฟ Probability Plot อาจจะมีประโยชน์ในการระบุค่าผิดปกติ (Outliers) หรือค่าที่แตกต่างจากค่าอื่นๆ ได้ โดยจุดต่างๆ ที่อยู่ตามแนวเส้นของกราฟ Probability Plot แสดงถึงค่าปกติทั่วไปที่เกิดจากการเปลี่ยนแปลงแบบสุ่ม ส่วนจุดที่อยู่ห่างออกจากบริเวณด้านบนหรือด้านล่างของปลายเส้น หรือมีจุดที่ห่างออกไปจากเส้น แสดงถึงค่าที่น่าสงสัย หรือค่าผิดปกติ (Outliers)
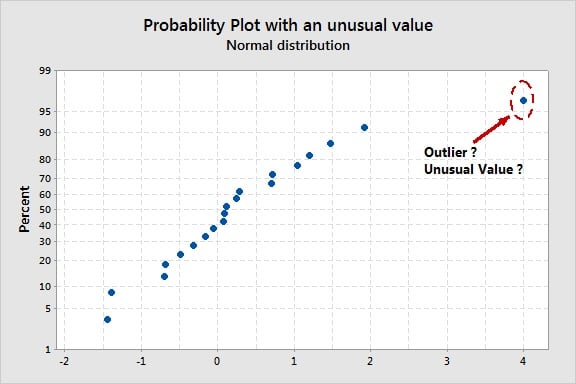
ค่าผิดปกติ (Outliers) อาจส่งผลกระทบอย่างมากกับโมเดล Regression หรือการวิเคราะห์ ANOVA เนื่องจากค่าผิดปกติเพียงค่าเดียว อาจทำให้ค่าสัมประสิทธิ์ของตัวทำนายทั้งหมดเกิดความเอนเอียงขึ้นได้ ดังนั้นกราฟ probability plot ของค่าเศษเหลือ (residual) จากโมเดลทางสถิติจึงมีประโยชน์อย่างมากในการตรวจสอบความถูกต้องของโมเดล และตรวจหาค่าผิดปกติ (outliers) บางค่าที่น่าจะเกิดจากความผิดพลาดในการทดสอบ หรือการวัดค่าที่ไม่ถูกต้อง ฯลฯ
กราฟ Probability plot ยังช่วยให้เข้าใจในเรื่องของการออกแบบการทดลองได้อีกด้วย สำหรับการวิเคราะห์ DOE (หรือการออกแบบการทดลอง) จะได้กราฟ effect plots ซึ่งก็คือ กราฟ Probability plot ที่แสดงผลกระทบของปัจจัย หรือ interaction ระหว่างปัจจัย กราฟเหล่านี้สามารถใช้เพื่อระบุว่าผลกระทบมีนัยสำคัญหรือไม่ หากผลกระทบที่อยู่ตามแนวเส้นของกราฟ Normal Probability Plot ถือว่าไม่มีนัยสำคัญ (ผลกระทบเหล่านี้เกิดจากการเปลี่ยนแปลงแบบสุ่มเท่านั้น) ในขณะที่จุดที่ดูเหมือนค่าผิดปกติแสดงให้เห็นว่า ผลกระทบมีนัยสำคัญอย่างแท้จริง
การใช้กราฟ Probability Plot เพื่อระบุการแจกแจงแบบไม่สมมาตร
ในกราฟด้านล่าง ข้อมูลถูกสร้างจากการแจกแจงแบบไม่สมมาตรอย่างมาก (เช่น การแจกแจง Exponential) จะเห็นได้ชัดเจนว่า จุดต่างๆ ไม่ได้อยู่ตามแนวเส้นกราฟ Probability Plot ของการแจกแจงปกติ และมีการกระจายตัวออกไปมากในบริเวณหางทางด้านขวาของกราฟ รวมถึงข้อมูลกระจุกรวมกันและอยู่ใกล้กันมากในบริเวณด้านซ้ายของการแจกแจง ทำให้ผลลัพธ์ที่ได้มีลักษณะเป็นเส้นโค้ง ไม่ใช่เส้นตรง
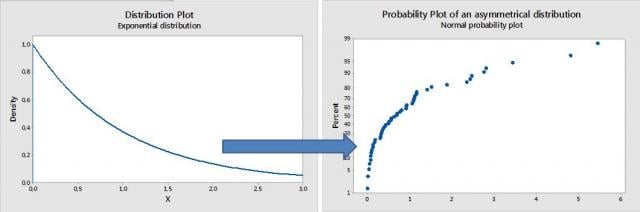
สิ่งนี้มีประโยชน์ต่อการวิเคราะห์ความสามารถ(capability analyses)ของกระบวนการ: เช่น รูปแบบเส้นโค้งดังกล่าว แสดงให้เห็นว่า การแจกแจงแบบไม่สมมาตรมีความเหมาะสมกว่า (ไม่ใช่การแจกแจงแบบปกติ) ซึ่งการประมาณค่า Cp และ Cpk มีความอ่อนไหวมากต่อข้อมูลที่ไม่ได้มีการแจกแจงปกติ
ในการออกแบบการทดลอง (DOE) หรือในการวิเคราะห์ Regression กราฟลักษณะนี้ แสดงให้เห็นว่า คุณจำเป็นต้องทำการแปลงข้อมูลให้มีการแจกแจงแบบปกติ หรือใช้การแจกแจงอื่นที่เหมาะสมกับข้อมูลของคุณมากกว่านี้
การใช้กราฟ Probability Plot เพื่อระบุการแจกแจงแบบไม่ต่อเนื่อง
ในกราฟด้านล่าง จะเห็นว่า จุดข้อมูลที่จับกลุ่มกันเป็นก้อนๆ อย่างชัดเจนตามแนวเส้นของกราฟ Probability Plot ซึ่งแสดงให้เห็นว่า ข้อมูลนี้ไม่ได้มีการแจกแจงแบบต่อเนื่อง (Continuous Distribution) ในการวิเคราะห์ระบบการวัด รูปแบบนี้มักจะบอกว่า เครื่องมือวัดของเรามีความละเอียดไม่เพียงพอ (เช่น แบ่งค่าได้ไม่กี่ระดับ) จริงๆ แล้วข้อมูลแต่ละจุดที่ดูใกล้เคียงกันในกราฟ อาจมีความแตกต่างกันเล็กน้อย แต่เครื่องมือวัดไม่สามารถตรวจจับความแตกต่างเล็กๆ น้อยๆ เหล่านั้นได้ ทำให้ผลลัพธ์ที่ได้กลายเป็นการกระจายตัวแบบไม่ต่อเนื่อง
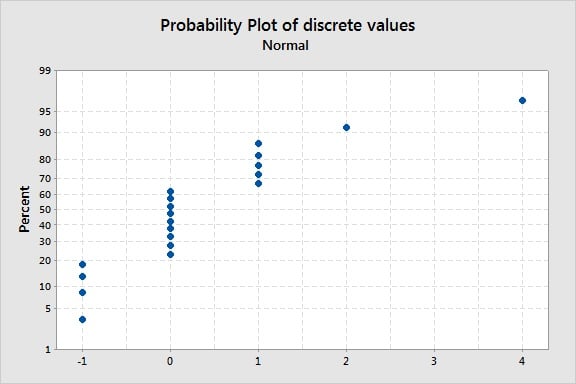
ตัวอย่าง: กราฟ Probability Plot โดยใช้ข้อมูลเกมเลเซอร์

เกมเลเซอร์กลายเป็นความบันเทิงที่ได้รับความนิยมอย่างมากในช่วงหลายปีที่ผ่านมา ผู้เล่นจะได้คะแนนจากการยิงเป้าด้วยอุปกรณ์อินฟราเรด หากยิงโดนผู้เล่นทีมตรงข้ามสำเร็จ จะทำให้ได้คะแนนเพิ่ม แต่ถ้าเผลอยิงพวกเดียวกันเอง หรือถูกทีมฝ่ายตรงข้ามยิง คะแนนก็จะลดลง ฉันได้เก็บข้อมูลคะแนนจากการเล่นเกมเลเซอร์หลายๆ รอบ เพื่อนำมาวิเคราะห์หารูปแบบในกราฟ Probability Plot ของคะแนนเหล่านี้ (นี่เป็นข้อมูลจริง ที่เก็บมาบางส่วนจากใบคะแนนของลูกชายฉันที่ชอบเล่นเกมเลเซอร์)
ในกราฟด้านล่างนี้ กราฟ Probability Plot ของเกมที่ 1 (มุมซ้ายด้านบน) มีค่าผิดปกติ (outlier) หรือค่าที่น่าสงสัยอย่างชัดเจน (กราฟแสดงให้เห็นว่า “ผู้เล่นยอดเยี่ยม (super player)” ที่ทำคะแนนได้โดดเด่นกว่าคนอื่นๆ อย่างเห็นได้ชัด)
ถึงแม้จะไม่มีค่าผิดปกติ (outlier) แต่โปรดสังเกตว่า ไม่สามารถลากเส้นดินสอหนา (Fat pencil) เพียงเส้นเดียวผ่านจุดทั้งหมดได้ ซึ่งเรามีกลุ่มที่แตกต่างกัน ดังนั้นจึงจำเป็นต้องใช้เส้น 3 เส้น โดย 3 จุดทางซ้าย แสดงถึงกลุ่มที่ทำผลงานต่ำกว่ามาตรฐาน ส่วนจุดทางขวา แสดงถึงกลุ่มที่ทำผลงานเกินมาตรฐาน และกลุ่มตรงกลาง แสดงถึงผู้เล่นที่มีผลงานอยู่ในระดับปกติ/เฉลี่ย โดยจุดที่อยู่บนเส้นเดียวกัน แสดงถึงความผันแปรแบบสุ่มภายในกลุ่ม (ภายใต้การแจกแจงแบบปกติ) อันเนื่องมาจาก ‘สาเหตุทั่วไป (common causes)’ และความแตกต่างระหว่างเส้นต่างๆ แสดงถึง ‘สาเหตุพิเศษ (special causes)’ ซึ่งมีความแตกต่างที่มีนัยสำคัญ โดยอาจเกิดจากเทคนิคการต่อสู้ที่แตกต่างกัน, ระดับความเชี่ยวชาญ, ความสามารถในการทำคะแนน หรือความก้าวหน้าในการเรียนรู้ของผู้เล่น เป็นต้น
เมื่อดูทั้งหมด 4 กราฟ จะเห็นได้ว่า สามารถแบ่งกลุ่มผู้เล่นได้หลายกลุ่มอย่างชัดเจน (ต้องใช้เส้นดินสอหนา (fat pencil) หลายเส้นในแต่ละกรณี)
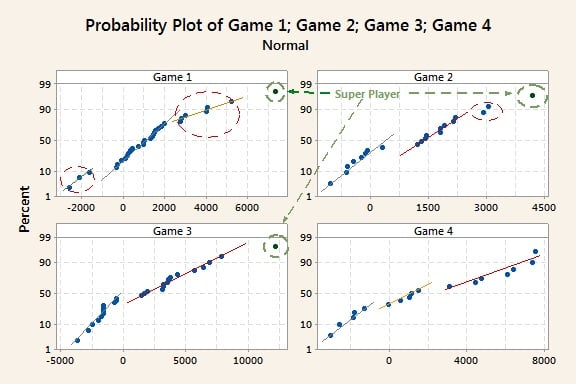
โปรดสังเกตว่า โดยทั่วไปเส้นสำหรับคะแนนที่ต่ำกว่ามาตรฐานจะมีความชันมากกว่า (มีการกระจายน้อยกว่าและข้อมูลกระจุกตัวมากกว่า) ในขณะที่ความชันของเส้นของกลุ่มที่ทำคะแนนเกินมาตรฐานที่อยู่ทางด้านขวาจะมีความชันที่น้อยกว่า และมีความผันแปรภายในกลุ่มมากกว่า
รูปแบบนี้แสดงว่า ค่าความผันแปรไม่คงที่ตามค่าเฉลี่ยของแต่ละกลุ่ม (ค่าเฉลี่ยยิ่งมาก ค่าความผันแปรของข้อมูลในแต่ละกลุ่มนั้นก็จะมากขึ้นด้วย โดยพฤติกรรมนี้ เราเรียกว่า “heteroscedasticity“)
สาเหตุที่เป็นเช่นนี้ อาจเป็นเพราะผู้เล่นที่ไม่มีประสบการณ์มักจะถูกยิงได้ง่ายและไม่สามารถแสดงศักยภาพที่แท้จริงได้อย่างเต็มที่ ในขณะที่ความแตกต่างของสไตล์และเทคนิคการเล่นมีบทบาทสำคัญกว่าผู้เล่นที่มีประสบการณ์มาก ดังนั้นเราจึงเห็นความแตกต่างที่มากระหว่างพวกเขาในแง่ของคะแนน
หากคุณเคยเห็นหรือเคยเล่นเกมเลเซอร์ คุณคงนึกภาพผู้เล่นมือใหม่ที่กำลังเดินอยู่ในพื้นที่มืดขนาดใหญ่และถูกเล็งเป้าโดยผู้เล่นที่มีประสบการณ์มากกว่า (ที่ซุ่มอยู่หลังที่กำบัง) และผู้เล่นมือใหม่ก็ไม่รู้ว่าจะไปทางไหนดี
กราฟเช่นนี้จะถูกตีความอย่างไรในสถานการณ์การปรับปรุงคุณภาพ?
การวิเคราะห์ความสามารถของกระบวนการ:ในการวิเคราะห์ความสามารถของกระบวนการ ถ้าเราเห็นเส้นดินสอหนา (Fat pencil) ที่แตกต่างกันหรือเส้นที่ขาดตอน แสดงว่า เราเอาชิ้นส่วนจากสายการผลิตอื่น หรือซัพพลายเออร์คนละเจ้า ฯลฯ มาผสมปนกัน จึงทำให้การแจกแจงข้อมูลโดยรวมไม่ได้มีการแจกแจงปกติ (และทำให้ค่า Cp กับ Cpk ที่คำนวณมีความเอนเอียง) เพราะจริงๆ แล้ว ข้อมูลเหล่านี้มาจากหลายๆ กลุ่ม ที่ข้อมูลในแต่ละกลุ่มมีการแจกแจงปกติ (แต่มีค่าเฉลี่ยไม่เท่ากัน) พอเอามาผสมปนกัน ผลที่ตามมาก็คือ อาจไม่มีการแจกแจงทางทฤษฎีใดๆ (เช่น การแจกแจงไวบูล หรือ ล็อกนอร์มอล) ที่จะเหมาะสมกับข้อมูลดังกล่าวได้ ฉะนั้น วิธีการวิเคราะห์ที่ซับซ้อนกว่า อาจเป็นทางออกในกรณีนี้ อย่างเช่น วิธีการวิเคราะห์แบบไม่อิงค่าพารามิเตอร์
การออกแบบการทดลอง:ในกราฟ effects plot ของการออกแบบการทดลอง (DOE) ค่าผิดปกติ (outlier) จะส่งผลต่อขนาดของผลกระทบที่การประมาณค่านั้นมีค่าสูงเกินไป (ถ้า level ที่แปลงรหัสเป็น 1 ในแถวของค่าผิดปกติ (outlier) สำหรับปัจจัยดังกล่าว) หรือการประมาณค่านั้นต่ำเกินไป (ถ้า level ที่แปลงรหัสเป็น -1 ในแถวของค่าผิดปกติ (outlier) สำหรับปัจจัยนั้นๆ) ผลที่ตามมาคือ เราจะเห็นเส้นดินสอหนา (Fat pencil) ที่มีความแตกต่างกัน หรือกลายเป็นเส้นที่ขาดตอนอีกครั้ง
การวิเคราะห์ความน่าเชื่อถือ: ในการวิเคราะห์ความน่าเชื่อถือ เส้นที่ขาดตอน มักเกิดจากรูปแบบของความล้มเหลวที่แตกต่างกัน ถึงแม้ว่าเราจะไม่ค่อยใช้การแจกแจงปกติในการวิเคราะห์ความน่าเชื่อถือ แต่กราฟ Probability Plot ของการแจกแจงไวบูลก็สามารถให้ผลลัพธ์ในลักษณะนี้เช่นกัน
บทสรุป
เกมเลเซอร์เป็นอะไรที่ยอดเยี่ยมตรงที่ให้ข้อมูลเรามากมายเลยทีเดียว ฉันขออวยพรให้ “ผู้เล่นยอดเยี่ยม (super player)” โชคดีในการเล่นรอบต่อไปนะ!
ดังที่คุณเห็น การพิจารณาผ่านรูปแบบของกราฟง่ายๆ ของกราฟ Probability Plot ก็ให้ข้อมูลเชิงลึกที่มีประโยชน์เกี่ยวกับโครงสร้างข้อมูล ซึ่งปริมาณข้อมูลกำลังเพิ่มขึ้นอย่างรวดเร็ว ไม่ว่าจะถูกสร้างขึ้นจากอินเทอร์เน็ต, จากอุปกรณ์อิเล็กทรอนิกส์, จากการจัดการความสัมพันธ์กับลูกค้า และจากเทคโนโลยีอื่นๆ ฉะนั้น การจดจำรูปแบบข้อมูลทั้งหมดนี้ ถือเป็นกุญแจสำคัญในการทำความเข้าใจกระบวนการของเรา รวมถึงลูกค้าของเรา ผลิตภัณฑ์ของเรา และโอกาสต่างๆ ของเราได้ดียิ่งขึ้น
ภาพถ่ายเลเซอร์ โดย Johannes Gilger, ใช้ภายใต้ใบอนุญาต Creative Commons 2.0
บทความต้นฉบับ : A Simple Guide to Probability Plots
ต้นฉบับนำมาจาก Minitab blog , แปลและเรียบเรียงโดยรัฐพงษ์ ยอดสีมา
บริหารจัดการ SCM Blog โดยชลทิชา จำรัสพร, บริษัท โซลูชั่น เซ็นเตอร์ จํากัด ตัวแทน Minitab ในประเทศไทย

เพิ่มเติมเกี่ยวกับบริษัท Minitab
Minitab ช่วยให้บริษัทและองค์กรต่างๆ สามารถมองเห็นแนวโน้มของข้อมูล, แก้ปัญหาและค้นพบประเด็นสำคัญจากข้อมูลเชิงลึก โดยนำเสนอชุดโซลูชั่นที่ครอบคลุมทุกด้านและดีที่สุดสำหรับซอฟต์แวร์ในระดับเดียวกัน ที่ใช้สำหรับการวิเคราะห์ข้อมูลและการปรับปรุงกระบวนการ
ด้วยวิธีการที่เป็นเอกลักษณ์ และการนำเสนอซอฟต์แวร์และบริการแบบองค์รวม Minitab ช่วยให้องค์กรเข้าถึงกระบวนการตัดสินใจในส่วนที่ช่วยผลักดันให้เกิดความเป็นเลิศทางธุรกิจได้ดีขึ้น ความง่ายในการใช้งานที่โดดเด่นกว่าใครมีส่วนช่วยให้ Minitab สามารถทำให้การเข้าถึงข้อมูลเชิงลึกเป็นเรื่องที่ง่าย ทีมงานของ Minitab ซึ่งประกอบด้วยผู้เชี่ยวชาญทางด้านการวิเคราะห์ข้อมูลที่ได้ผ่านการอบรมมาเป็นอย่างเข้มงวด จะช่วยให้ผู้ใช้งานมั่นใจว่าจะได้รับประโยชน์สูงสุดจากการใช้งานวิเคราะห์ข้อมูลและพร้อมที่จะให้คำปรึกษาตลอดเวลาที่ใช้งานเพื่อนำไปสู่การตัดสินใจที่ดีขึ้น รวดเร็ว และแม่นยำ
เป็นเวลากว่า 50 ปีที่ Minitab ได้ช่วยองค์การต่าง ๆ เพิ่มรายได้ ควบคุมและลดต้นทุน เพิ่มคุณภาพ เสริมสร้างความพึงพอใจของลูกค้า และเพิ่มประสิทธิภาพ ธุรกิจและองค์นับหมื่นทั่วโลกใช้ Minitab Statistical Software®, Companion by Minitab®, Minitab Workspace®, Salford Predictive Modeler® and Quality Trainer® เป็นเครื่องมือช่วยในการค้นพบและปรับปรุงความบกพร่องในกระบวนการ

