ในบทความที่แล้ว เราได้ระบุการแจกแจงของข้อมูลไขมันในร่างกาย(body fat data) แต่ในวันนี้ เราจะมาค้นหาประโยชน์ต่าง ๆ ที่ได้จากการรู้การแจกแจงของข้อมูล โดยเฉพาะอย่างยิ่งกับการสร้างกราฟที่ให้ข้อมูลนั้น! และท้ายที่สุด หากคุณไม่แน่ใจว่า การแจกแจงที่เฉพาะเจาะจงกับพารามิเตอร์ดังกล่าวมีลักษณะอย่างไร กราฟจะให้สิ่งนั้นแก่คุณ!
.
.
การใช้ข้อมูลจากการแจกแจง
จนถึงตอนนี้ เราได้ระบุการแจกแจงและค่าพารามิเตอร์สำหรับข้อมูลไขมันในร่างกายจากเด็กผู้หญิงที่มีอายุ 14 ปี
การแจกแจงแบบไวบูลที่มี 3 พารามิเตอร์
- Shape = 1.85718
- Scale = 14.07043
- Threshold = 16.06038
สิ่งนี้ช่วยเราได้อย่างไร? แล้วนี่มันมีรูปร่างหน้าตายังไง? และช่วงของไขมันในร่างกายที่เหมาะสมกับการแจกแจงนี้จะตกอยู่ตำแหน่งไหน? ซึ่งคุณไม่สามารถบอกได้เพียงแค่ดูค่าพารามิเตอร์ แต่อย่างไรก็ตาม ฉันจะตอบคำถามเหล่านี้ด้วยกราฟเจ๋ง ๆ เพียงกราฟเดียว!
นับว่าเป็นวิธีการที่ดี ที่เราได้รู้การแจกแจงข้อมูลของคุณก่อนที่จะวิเคราะห์ ซึ่งบางการวิเคราะห์จำเป็นต้องรู้การแจกแจงก่อน ตัวอย่างเช่น การใช้ข้อมูลที่ไม่ได้มีการแจกแจงแบบปกติ มันอาจเป็นความผิดพลาดที่ร้ายแรงในการใช้การวิเคราะห์ใดการวิเคราะห์หนึ่งที่จำเป็นต้องมีการแจกแจงปกติอย่างเคร่งครัด แต่อย่างไรก็ตาม ฉันไม่พูดถึงตัวเลือกการวิเคราะห์แบบอื่น ๆ แต่ฉันจะพูดถึงกราฟและสิ่งที่เราสามารถทำได้เพียงแค่ได้จากการรู้การแจกแจงของข้อมูล
เนื่องจากเราได้ทำการระบุการแจกแจงที่เหมาะสมที่สุดมาแล้ว ซึ่งเราไม่ได้ถูกจำกัดแค่อธิบายเฉพาะข้อมูลตัวอย่างเท่านั้น ตอนนี้เราสามารถอนุมานเกี่ยวกับประชากรได้อีกด้วย ก็เหมือนกับการที่เราสร้างกราฟ Histogram จากบทความที่แล้วนั่นแหละ โดยที่เราสามารถสร้างกราฟที่ประมาณค่าที่ดีที่สุดสำหรับลักษณะของประชากรทั้งหมด และคำนวณความน่าจะเป็นสำหรับค่าที่อยู่ในช่วงที่กำหนดได้ งั้นมาเริ่มทำกันเลย
กราฟ Probability Distribution Plot
เพื่อตอบคำถามทั้งหมดของเรา เราจะใช้กราฟ Probability Distribution Plot ด้วยโปรแกรม Minitab ซึ่งฉันเป็นแฟนพันธุ์แท้ของกราฟเหล่านี้ หากคุณต้องการแสดงให้เจ้านายเห็นว่า การแจกแจงของข้อมูลที่มีลักษณะผิดแปลกที่มีชื่อพารามิเตอร์ที่เข้าใจยากนั้นมีลักษณะอย่างไร ให้ใช้กราฟนี้ช่วยอธิบาย โดยคุณสามารถเน้นไปที่ผลกระทบจากการแจกแจงของข้อมูลที่เปลี่ยนแปลงและค่าพารามิเตอร์ต่าง ๆ รวมทั้งแสดงค่าเป้าหมายที่ตกอยู่ในตำแหน่งหนึ่งของการแจกแจง และดูสัดส่วนจากค่าเป้าหมายผ่านพื้นที่ใต้กราฟ ซึ่งกราฟง่าย ๆ เหล่านี้เอง ก็สามารถสื่อสารแนวคิดสถิติขั้นสูงให้กับผู้ฟังที่ไม่ใช่นักสถิติได้อย่างง่ายดายและชัดเจน
กราฟ Probability Distribution Plot ไม่ต้องใช้ข้อมูลใด ๆ ซึ่งคุณเพียงแค่ระบุการแจกแจงของข้อมูลและป้อนค่าพารามิเตอร์เข้าไป คุณก็สามารถระบุพื้นที่ใต้กราฟที่คุณสนใจได้
เราจะใช้ค่าพารามิเตอร์จากประชากรที่เราได้บอกก่อนหน้านี้ สำหรับพื้นที่ใต้กราฟที่เราสนใจ ฉันไปเจอมาในเว็บไซต์แห่งหนึ่งได้แนะนำว่า เด็กผู้หญิงที่มีอายุระหว่าง 14-19 ปี ตามหลักการด้านสุขภาพแล้ว พวกเขาควรมีเปอร์เซ็นต์ไขมันในร่างกายระหว่าง 20%-24% ซึ่งในความคิดของฉันคิดว่า ช่วงดังกล่าวนั้นฟังดูแคบมาก แต่ลองมาดูกันว่า มันจะตกอยู่ที่ตำแหน่งใดในการแจกแจงของประชากรของไขมันในร่างกายสำหรับเด็กผู้หญิงที่มีอายุ 14 ปี
ในโปรแกรม Minitab ฉันจะไปที่เมนู Graph > Probability Distribution Plot > View Probability และป้อนข้อมูลการแจกแจงของเราใน dialog หลักดังนี้:
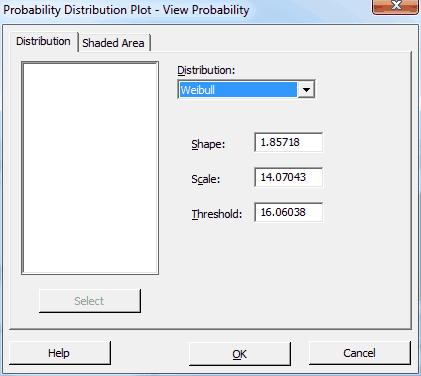
จากนั้น ฉันจะคลิกแท็บ Shaded Area และกรอกข้อมูลดังนี้:
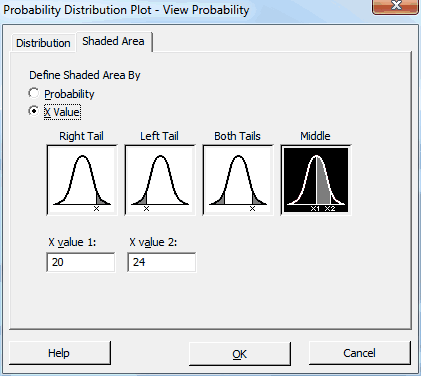
หลังจากนั้น เราคลิก OK แล้วโปรแกรม Minitab จะแสดงกราฟต่อไปนี้:
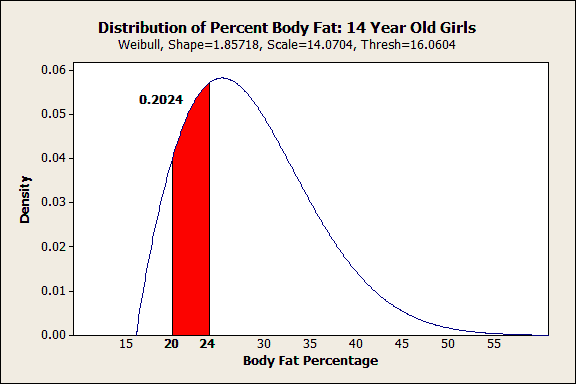
เพียงแค่กราฟเดียว คุณจะเห็นทั้งรูปร่างของการแจกแจง และช่วงของเปอร์เซ็นต์ไขมันในร่างกายที่เราสนใจนั้นเหมาะสมได้อย่างไร แน่นอนฉันไม่ใช่ผู้เชี่ยวชาญด้านสุขภาพ แต่ฉันเห็นว่า ช่วงเปอร์เซ็นต์ไขมันในร่างกายตามอุดมคติจากเว็บไซต์ ไม่ได้สะท้อนให้เห็นว่า เด็กผู้หญิงส่วนใหญ่มีเปอร์เซ็นต์ไขมันเป็นเท่าใด ซึ่งมีเพียง 20% เท่านั้นที่อยู่ในช่วงดังกล่าว และมันก็อยู่ใต้ตำแหน่งที่สูงที่สุดของเส้นโค้ง ซึ่งมันมีอะไรบางอย่างที่น่าสนใจ
กราฟ Probability Plots เพื่อคำนวณเปอร์เซ็นต์ไทล์
กราฟ Probability Plots มีชื่อคล้ายกันกับกราฟ Probability Distribution Plots โดยทั้งสองกราฟมีความเกี่ยวข้องกัน แต่กราฟ Probability Plots นั้นมีข้อดีเป็นพิเศษในการพิจารณาว่า ข้อมูลนั้นเหมาะสมกับการแจกแจงหรือไม่ (ซึ่งเราได้ทำการตรวจสอบเป็นที่เรียบร้อยแล้ว) และคำนวณเปอร์เซ็นต์ไทล์ตามการแจกแจงนั้น โดยทั่วไปเปอร์เซ็นต์ไทล์ที่ n หมายถึง มี n% ของประชากรที่มีค่าน้อยกว่าค่าที่กำหนด และมี (100-n)% ของประชากรที่มีค่ามากกว่าค่าที่กำหนด
เปอร์เซ็นต์ไทล์มีความสำคัญเป็นพิเศษสำหรับการแจกแจงอื่น ๆ ที่ไม่ใช่การแจกแจงแบบปกติ และนี่คือเหตุผล เนื่องจากคุณใช้เปอร์เซ็นต์ไทล์ เพื่อค้นหาจุดศูนย์กลางและการกระจายตัวของการแจกแจงของคุณ
ตามสัญชาตญาณ เราคิดว่าค่าเฉลี่ยและค่าเบี่ยงเบนมาตรฐานเป็นจุดศูนย์กลางและการกระจายตัวสำหรับการแจกแจงแบบปกติ ยิ่งไปกว่านั้น กฎทั่วไปสำหรับการแจกแจงแบบปกติที่ดี คือ 2 ใน 3 ของประชากรตกอยู่ในตำแหน่งภายใน 1 ส่วนเบี่ยงเบนมาตรฐานจากค่าเฉลี่ยอย่างสมมาตร และประมาณ 95% ตกอยู่ในตำแหน่งภายใน 2 ส่วนเบี่ยงเบนมาตรฐาน
แต่อย่างไรก็ตาม สิ่งนี้ไม่เป็นความจริงสำหรับการแจกแจงที่ไม่สมมาตร โดยค่าเฉลี่ยไม่ได้อยู่ที่จุดศูนย์กลาง และกฎทั่ว ๆ ไป สำหรับการกระจายตัวนั้นไม่สามารถใช้การได้ ในขณะเดียวกัน เมื่อคุณระบุการแจกแจงของคุณได้แล้ว คุณก็สามารถคำนวณเปอร์เซ็นต์ไทล์ เพื่อหาจุดศูนย์กลางและการกระจายตัวของประชากรได้เช่นกัน
ตัวอย่างเช่น หากคุณต้องการหาค่ากลาง (มัธยฐาน) และช่วงกึ่งกลางที่ 95% ของประชากรที่ไม่ใช่การแจกแจงปกติ โดยคำนวณเปอร์เซ็นต์ไทล์ที่ 2.5, 50 และ 97.5 (จะได้ว่า 97.5 – 2.5 = 95) ซึ่งค่ามัธยฐาน คือ เปอร์เซ็นต์ไทล์ที่ 50 หมายถึง สัดส่วนครึ่งหนึ่งของประชากรทั้งหมดจะมีค่ามากกว่าค่ามัธยฐานและอีกครึ่งหนึ่งจะมีค่าน้อยกว่า
เราจะคำนวณเปอร์เซ็นต์ไขมันในร่างกายที่สอดคล้องกับเปอร์เซ็นต์ไทล์ที่ 2.5, 50 และ 97.5 รวมทั้งมาดูกันว่า เปอร์เซ็นต์ไทล์ใดที่สอดคล้องกับขอบเขตบนของช่วงของไขมันในร่างกายตามอุดมคติที่ 24%
ในการดำเนินการนี้ คุณจะต้องเปิดข้อมูล ซึ่งสามารถดาวน์โหลดได้ที่นี่
- ในโปรแกรม Minitab ไปที่เมนู Graph > Probability Plot > Single
- ใน dialog หลัก ให้ป้อน %Fat ลงใน Graph Variable
- คลิกปุ่มDistribution และเลือก 3-parameter Weibull แล้วคลิก OK
- คลิกปุ่ม Scale และในช่องทำเครื่องหมาย ให้ยกเลิกการเลือก Adjust x-scale for threshold . . ซึ่งสิ่งนี้จะสร้างเส้นโค้งการแจกแจงที่เหมาะสม และสามารถอ่านค่าเปอร์เซ็นต์ไทล์จากกราฟได้โดยตรง
- ยังอยู่ภายใต้ปุ่ม Scale เช่นเดิม ให้คลิกแท็บ Percentile Lines และกรอกข้อมูลตามรูปภาพที่แสดงด้านล่าง เพื่อคำนวณเปอร์เซ็นต์ไทล์ตามที่ต้องการ แล้วคลิก OK ใน dialog ทั้งหมด
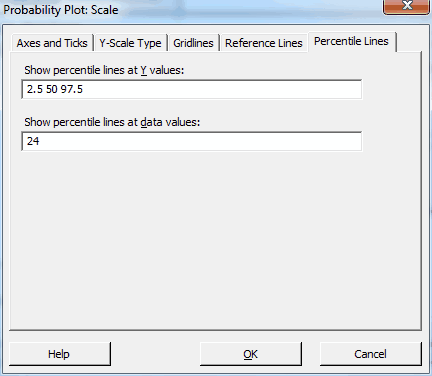
เราได้รับกราฟต่อไปนี้:
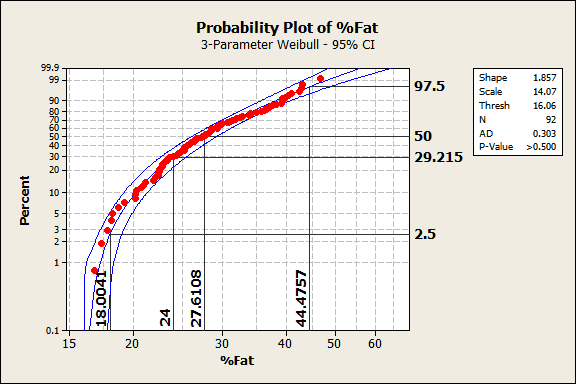
เรารู้อยู่แล้วว่า ข้อมูลเหล่านี้เป็นไปตามการแจกแจงแบบไวบูลที่มี 3 พารามิเตอร์จากบทความก่อนหน้านี้ และผลลัพธ์ที่ได้ก็ยืนยันอีกครั้งว่า ทั้งข้อมูลในแต่ละจุดอยู่ในระนาบเส้นกึ่งกลาง และในช่องคำอธิบายด้านขวามือ ค่า p-value มากกว่า 0.500 ซึ่งมากกว่าค่าอัลฟาที่กำหนดทั่ว ๆ ไป ดังนั้น ข้อมูลเหล่านี้จึงเป็นไปตามการแจกแจงแบบไวบูลที่มี 3 พารามิเตอร์
ในกราฟ ค่าข้อมูลที่อยู่บนแกน X และค่าเปอร์เซ็นต์ไทล์ที่อยู่บนแกน Y สำหรับประชากรกลุ่มนี้ ซึ่งเปอร์เซ็นต์ไทล์ที่ 50 (ค่ามัธยฐาน) สอดคล้องกับเปอร์เซ็นต์ไขมันในร่างกายที่มีค่าเท่ากับ 27.6% ในขณะที่ 95% ของประชากรที่มีค่าอยู่ระหว่างเปอร์เซ็นต์ไทล์ที่ 2.5 ถึง 97.5 สอดคล้องกับไขมันในร่างกายที่ 18.0% ถึง 44.5% เนื่องจากการแจกแจงที่รูปร่างที่ไม่สมมาตร ค่ามัธยฐาน (27.6) จึงอยู่ใกล้ค่าเปอร์เซ็นต์ไทล์ที่ต่ำมากกว่าค่าสูง
โดย 24% ของไขมันในร่างกาย ซึ่งเป็นขอบเขตบนของช่วงของไขมันในร่างกายตามอุดมคติที่เว็บไซต์ได้แนะนำ สอดคล้องกับเปอร์เซ็นต์ไทล์ที่ 29 แต่มันเป็นเปอร์เซ็นต์ไทล์ที่ค่อนข้างต่ำสำหรับประชากรกลุ่มนี้ กล่าวอีกนัยหนึ่งคือ มี 71% ของประชากรมีไขมันในร่างกายเกินกว่าขอบเขตบนของช่วงดังกล่าว อุ๊ย!
บทส่งท้าย
สำหรับปัญหาที่เกี่ยวข้องกับช่วงไขมันในร่างกายตามอุดมคติ มันค่อนข้างชัดเจนว่ามีบางอย่างเกิดขึ้นในการวิเคราะห์นี้ ซึ่งฉันไม่ใช่ผู้เชี่ยวชาญด้านสุขภาพ ดังนั้นฉันจึงไม่ทราบคำตอบ แต่อย่างไรก็ตาม มันปรากฏว่าช่วงใดช่วงหนึ่งนั้นไม่ถูกต้อง หรือเด็กผู้หญิงอายุ 14 ปีส่วนใหญ่ (71%) มีไขมันในร่างกายเกินกว่าช่วงที่แนะนำ ซึ่งมีเพียง 20% เท่านั้นที่อยู่ในช่วงที่กำหนด อย่างไรก็ดี ด้วยเครื่องมือง่าย ๆ ไม่กี่เครื่องมือในโปรแกรม Minitab เราสามารถนำความหมายของข้อมูลเหล่านี้มาสู่ความเป็นจริงได้! และที่สำคัญไม่แพ้กัน เราสามารถนำเสนอผลลัพธ์เหล่านี้ให้กับผู้อื่นได้อย่างง่ายดายด้วยรูปแบบที่เข้าใจง่ายได้อีกด้วย
ฉันหวังว่าหลังจากอ่านข้อความนี้ คุณจะสบายใจมากขึ้นกับการแจกแจงอื่น ๆ ที่ไม่ใช่การแจกแจงแบบปกติ และสามารถเห็นข้อดีของการระบุการแจกแจงข้อมูลของคุณ โดยฉันได้แสดงวิธีการที่คุณสามารถมองข้ามข้อมูลตัวอย่างของคุณ และทำการอนุมานที่เป็นประโยชน์เกี่ยวกับประชากรที่มีขนาดใหญ่ขึ้น โดยมีข้อมูลของคุณเป็นตัวแทนของประชากร ซึ่งคุณสามารถนำข้อมูลที่ไม่ได้มีการแจกแจงแบบปกติของคุณมาใช้ได้อย่างปลอดภัย!
บทความต้นฉบับ : The Graphical Benefits of Identifying the Distribution of Your Data
ต้นฉบับนำมาจาก Minitab blog, แปลและเรียบเรียงโดยรัฐพงษ์ ยอดสีมา
บริหารจัดการ SCM Blog โดยชลทิชา จำรัสพร, บริษัท โซลูชั่น เซ็นเตอร์ จํากัด ตัวแทน Minitab ในประเทศไทย

เพิ่มเติมเกี่ยวกับบริษัท Minitab
Minitab ช่วยให้บริษัทและองค์กรต่างๆ สามารถมองเห็นแนวโน้มของข้อมูล, แก้ปัญหาและค้นพบประเด็นสำคัญจากข้อมูลเชิงลึก โดยนำเสนอชุดโซลูชั่นที่ครอบคลุมทุกด้านและดีที่สุดสำหรับซอฟต์แวร์ในระดับเดียวกัน ที่ใช้สำหรับการวิเคราะห์ข้อมูลและการปรับปรุงกระบวนการ
ด้วยวิธีการที่เป็นเอกลักษณ์ และการนำเสนอซอฟต์แวร์และบริการแบบองค์รวม Minitab ช่วยให้องค์กรเข้าถึงกระบวนการตัดสินใจในส่วนที่ช่วยผลักดันให้เกิดความเป็นเลิศทางธุรกิจได้ดีขึ้น ความง่ายในการใช้งานที่โดดเด่นกว่าใครมีส่วนช่วยให้ Minitab สามารถทำให้การเข้าถึงข้อมูลเชิงลึกเป็นเรื่องที่ง่าย ทีมงานของ Minitab ซึ่งประกอบด้วยผู้เชี่ยวชาญทางด้านการวิเคราะห์ข้อมูลที่ได้ผ่านการอบรมมาเป็นอย่างเข้มงวด จะช่วยให้ผู้ใช้งานมั่นใจว่าจะได้รับประโยชน์สูงสุดจากการใช้งานวิเคราะห์ข้อมูลและพร้อมที่จะให้คำปรึกษาตลอดเวลาที่ใช้งานเพื่อนำไปสู่การตัดสินใจที่ดีขึ้น รวดเร็ว และแม่นยำ
เป็นเวลากว่า 50 ปีที่ Minitab ได้ช่วยองค์การต่าง ๆ เพิ่มรายได้ ควบคุมและลดต้นทุน เพิ่มคุณภาพ เสริมสร้างความพึงพอใจของลูกค้า และเพิ่มประสิทธิภาพ ธุรกิจและองค์นับหมื่นทั่วโลกใช้ Minitab Statistical Software®, Companion by Minitab®, Minitab Workspace®, Salford Predictive Modeler® and Quality Trainer® เป็นเครื่องมือช่วยในการค้นพบและปรับปรุงความบกพร่องในกระบวนการ