การทดสอบ t-test เป็นการทดสอบสมมติฐานทางสถิติที่มีประโยชน์เมื่อคุณต้องการเปรียบเทียบค่าเฉลี่ย คุณสามารถเปรียบเทียบค่าเฉลี่ยของตัวอย่างกับสมมติฐานหลักหรือค่าเป้าหมายโดยการใช้ 1 sample t-test คุณสามารถเปรียบเทียบค่าเฉลี่ยของสองกลุ่มตัวอย่างด้วย 2 sample t-test ถ้าคุณมีสองกลุ่มที่เป็นคู่ทดสอบ (เช่น ก่อนและหลังการวัด) ใช้การทดสอบ Paired t-test
การทดสอบ t-test ทำงานอย่างไร? ค่า t-value เท่าไหร่เหมาะสม? ในบทความชุดนี้ฉันจะตอบคำถามเหล่านี้โดยเน้นที่แนวคิดและกราฟมากกว่าสมการและตัวเลข ท้ายที่สุดเหตุผลสำคัญในการใช้ซอฟต์แวร์ทางสถิติเช่น Minitab คือคุณจะไม่ไปเสียเวลาอยู่กับการคำนวณแต่สามารถมุ่งเน้นไปที่การทำความเข้าใจผลลัพธ์ของคุณแทน
ในโพสต์นี้ฉันจะอธิบายค่า t-value, การแจกแจง t (t-distribution) และการทดสอบ t-test มีวิธีการคำนวณหาความน่าจะเป็นและประเมินสมมติฐานอย่างไร
ค่า t-value คืออะไร?
การทดสอบ t-test ที่เรียกว่าการทดสอบ t-test เพราะว่าผลการทดสอบทั้งหมดขึ้นอยู่กับค่า t-value สิ่งที่นักสถิติเรียกมันเป็นการทดสอบทางสถิติ การทดสอบทางสถิติคือค่ามาตรฐานที่คำนวณจากข้อมูลตัวอย่างในระหว่างการทดสอบสมมติฐาน ขั้นตอนที่คำนวณค่าสถิติสำหรับการทดสอบจะเปรียบเทียบข้อมูลของคุณกับสิ่งที่คาดหวังที่กำหนดไว้ในสมมติฐานหลัก(null hypothesis)
การทดสอบ t-test แต่ละประเภทใช้ขั้นตอนในการลดข้อมูลตัวอย่างทั้งหมดของคุณให้เหลือค่าเดียวคือค่า t-value การคำนวณจะเปรียบเทียบค่าเฉลี่ยตัวอย่างของคุณกับสมมติฐานหลักและรวมถึงพิจารณาทั้งขนาดตัวอย่างและความแปรปรวนในข้อมูล ค่า t-value เป็น 0 หมายถึงว่าค่าประมาณของตัวอย่างเท่ากับสมมติฐานหลักทุกประการ ในทางสถิติเราเรียกความแตกต่างระหว่างค่าประมาณตัวอย่างและสมมติฐานหลักว่าขนาดผลกระทบ เมื่อความแตกต่างนี้เพิ่มขึ้นค่าสัมบูรณ์(absolute)ของค่า t-value จะเพิ่มขึ้น
สมมติว่าเราทำการทดสอบ t-test และคำนวณได้ค่า t-value เท่ากับ 2 จากข้อมูลตัวอย่างของเรา นั่นหมายความว่าอย่างไร? ฉันอาจบอกคุณเช่นกันว่าข้อมูลของเราเท่ากับ 2 ฟิซบิน(fizbins)! เราไม่รู้ว่าเป็นเรื่องธรรมดาหรือเป็นไปได้ยากเมื่อสมมติฐานหลักเป็นจริง
โดยตัวของมันเองค่า t-value เท่ากับ 2 ไม่ได้บอกอะไรเราเลย ค่า t-value ไม่ได้อยู่ในหน่วยของข้อมูลดั้งเดิมหรืออย่างอื่นที่เราคุ้นเคย เราต้องการบริบทที่ใหญ่ขึ้นซึ่งเราต้องเหลือค่า t-value เดี่ยวๆก่อนที่จะตีความได้ นี่คือที่มาของการแจกแจง t-distribution
การแจกแจง t-Distributions คืออะไร?
เมื่อคุณทำการทดสอบ t-test คุณทำการศึกษาเพียงครั้งเดียวคุณจะได้ค่า t-value เพียงค่าเดียว แต่ถ้าหากคุณสุ่มหลายๆตัวอย่างที่มีขนาดเท่ากันจากประชากรกลุ่มเดียวกันและทำการทดสอบ t-test คุณจะได้ค่า t-value หลายๆตัวซึ่งเราสามารถพล็อตการแจกแจงค่าเหล่านั้นทั้งหมดได้ เราเรียกการแจกแจงแบบนี้ว่า การแจกแจงตัวอย่างสุ่ม(sampling distribution)
โชคดีที่คุณสมบัติของการแจกแจง t-distribution เป็นที่เข้าใจกันดีในทางสถิติดังนั้นเราจึงสามารถพล็อตได้โดยไม่ต้องเก็บตัวอย่างมากมาย! การแจกแจงแบบ t-distribution ที่เลือกใช้ถูกกำหนดโดยองศาอิสระ (DF-degree of freedom) ซึ่งเป็นค่าที่เกี่ยวข้องอย่างใกล้ชิดกับขนาดตัวอย่าง ดังนั้นจึงมีการแจกแจง t-test ที่แตกต่างกันสำหรับทุกขนาดตัวอย่าง คุณสามารถสร้างกราฟการแจกแจง t-distribution โดยใช้พล็อตการแจกแจงความน่าจะเป็นของ Minitab(probability distribution plots)
การแจกแจง t-distribution มีสมมติฐานว่าคุณทำการสุ่มตัวอย่างซ้ำๆจากประชากรที่สมมติฐานหลักเป็นจริง คุณนำค่า t-value ที่ได้จากการศึกษาของคุณวางลงบนการแจกแจง t-distribution เพื่อหาว่าผลลัพธ์ของคุณสอดคล้องกับสมมติฐานหลักเพียงใด
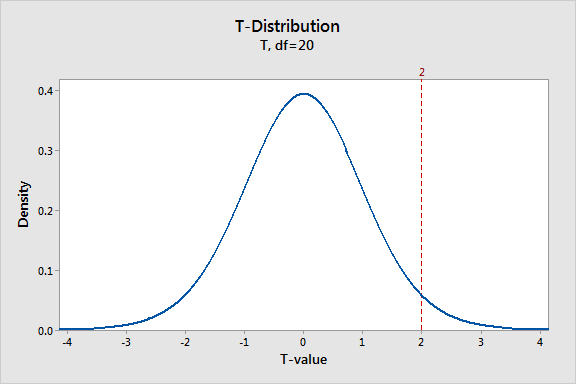
กราฟด้านบนแสดงการแจกแจง t-distribution ที่มีองศาอิสระ(df) เท่ากับ 20 ซึ่งมาจากขนาดตัวอย่างเท่ากับ 21 ใช้ในการทดสอบ 1 sample t-test
จุดสูงสุดของกราฟอยู่ที่ค่าศูนย์ ซึ่งหมายความว่าค่าที่ได้จากตัวอย่างใกล้เคียงกับสมมติฐานหลักมากที่สุด สมเหตุสมผลเพราะการแจกแจงแบบ t-distribution มีสมมติฐานว่าสมมติฐานหลักเป็นจริง ค่า t-value ของคุณจะมีโอกาสเป็นจริงน้อยลงเมื่ออยู่ห่างจากศูนย์ในทิศทางใดทิศทางหนึ่งก็ได้ กล่าวอีกนัยหนึ่งคือถ้าสมมติฐานหลักเป็นจริง โอกาสของคุณน้อยมากเพราะค่าที่ได้มันแตกต่างหรือไกลจากสมมติฐานหลักมาก
ค่า t-value เท่ากับ 2 หมายความถึงความแตกต่างในเชิงบวกระหว่างข้อมูลตัวอย่างของเรากับสมมติฐานหลัก กราฟแสดงให้เห็นว่าโอกาสของค่า t-value จาก -2 ถึง +2 จะเป็นจริงเมื่อสมมติฐานหลักเป็นจริง ค่า t-value เท่ากับ 2 เป็นค่าที่เบี่ยงเบนออกมา(จากค่าศูนย์) แต่เราไม่รู้ว่าแท้จริงแล้วมันเบี่ยงเบนออกมาเนื่องจากอะไร เป้าหมายสูงสุดของเราคือการพิจารณาว่าค่า t-value ที่เบี่ยงเบนออกมานั้นเพียงพอที่จะรับประกันได้เมื่อเราปฏิเสธสมมติฐานหลัก ในการทำเช่นนั้นเราจะต้องคำนวณหาความน่าจะเป็น
การใช้ค่า t-value และ t-distribution ในการคำนวณหาความน่าจะเป็น
จุดเริ่มต้นเบื้องหลังของการทดสอบสมมติฐานใดๆคือใช้การทดสอบทางสถิติจากกลุ่มตัวอย่างและวางไว้ในบริบทของการแจกแจงความน่าจะเป็นที่ทราบ สำหรับการทดสอบ t-test หากคุณใช้ค่า t-test และวางไว้ในบริบทของการแจกแจง t-distribution ที่ถูกต้อง คุณสามารถคำนวณค่าความน่าจะเป็นของค่า t-value จากการแจกแจงนั้นได้
ความน่าจะเป็นช่วยให้เราสามารถระบุได้ว่าค่า t-value ของเราเป็นปกติหรือมีโอกาสน้อยที่จะเป็นจริงภายใต้สมมติฐานที่ว่าสมมติฐานหลักเป็นจริง ถ้าหากความน่าจะเป็นต่ำเพียงพอเราสามารถสรุปได้ว่าค่าที่ได้จากตัวอย่างของเราไม่สอดคล้องกับสมมติฐานหลัก หลักฐานจากข้อมูลตัวอย่างอธิบายประชากรได้ทั้งหมดว่ามีความชัดเจนเพียงพอที่จะปฏิเสธสมมติฐานหลัก
ก่อนที่เราจะคำนวณความน่าจะเป็นที่ได้ค่า t-value เท่ากับ 2 มานั้นมีรายละเอียดสำคัญสองประการที่ต้องอธิบาย:
ประการแรก, จริงๆแล้วเราจะใช้ค่า t-value ทั้ง +2 และ -2 เพราะว่าเราทำการทดสอบแบบสองด้าน การทดสอบแบบสองด้านคือการทดสอบความแตกต่างของทั้งสองทิศทาง ตัวอย่างเช่น การทดสอบ 2 sample t-test แบบสองด้านสามารถหาได้ว่าความแตกต่างระหว่างกลุ่ม 1 และกลุ่ม 2 มีนัยสำคัญทางสถิติในทิศทางบวกหรือลบ การทดสอบด้านเดียวสามารถประเมินทิศทางเหล่านั้นได้เพียงด้านเดียว
ประการที่สอง, เราสามารถคำนวณเพียงความน่าจะเป็นที่ไม่มีทางเป็นศูนย์สำหรับช่วงของค่า t-value เท่านั้น ดังที่คุณจะเห็นในกราฟด้านล่างช่วงของค่า t-value จะสอดคล้องกับสัดส่วนของพื้นที่ทั้งหมดภายใต้เส้นโค้งการแจกแจงซึ่งก็คือความน่าจะเป็นนั่นเอง ค่าความน่าจะเป็นของค่าที่จุดใดๆจะเท่ากับศูนย์เสมอเพราะมันไม่สามารถหาค่าพื้นที่ใต้กราฟได้
เมื่อเราพิจารณาถึงประเด็นเหล่านี้เราจะแรเงาพื้นที่ใต้กราฟที่มีค่า t-value มากกว่า 2 และค่า t-value น้อยกว่า -2
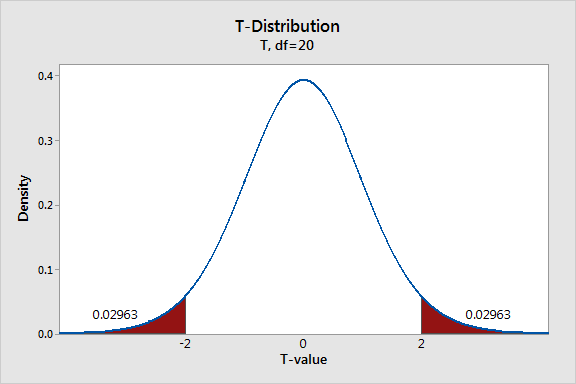
กราฟแสดงความน่าจะเป็นน้อยที่สุดของค่าที่ได้จากข้อมูลต่างจากสมมติฐานหลักจะเป็นจริงเมื่อสมมติฐานหลักเป็นจริง พื้นที่ที่แรเงาแต่ละด้านมีค่าความน่าจะเป็น 0.02963 รวมกันแล้วความน่าจะเป็นเท่ากับ 0.05926 เมื่อสมมติฐานเป็นจริงค่า t-value แต่ละครั้งจะตกบนพื้นที่เหล่านี้ใกล้เคียง 6%
ความน่าจะเป็นนี้มีชื่อที่คุณอาจเคยได้ยินมาแล้วมันเรียกว่าค่า p-value แม้ว่าความน่าจะเป็นที่ค่า t-value ของเราจะตกในพื้นที่ดังกล่าวจะค่อนข้างต่ำ แต่ก็ยังไม่ต่ำพอที่จะปฏิเสธสมมติฐานหลักถ้าเราใช้ระดับนัยสำคัญ(significance level)ที่ใช้ทั่วไปที่ 0.05
เรียนรู้เรื่องการแปลผลค่า P-value ได้อย่างถูกต้องได้จากบทความ Learn how to correctly interpret the p-value (เราเตรียมที่จะแปลบทความนี้เร็วๆนี้)
การแจกแจง t-distribution และขนาดสิ่งตัวอย่าง
ดังที่ได้กล่าวมาแล้วก่อนหน้านี้ การแจกแจง t-distribution ถูกกำหนดโดยองศาอิสระ(degree of freedom) หรือ DF ซึ่งมีความสัมพันธ์อย่างมากกับขนาดตัวอย่าง เมื่อ DF เพิ่มขึ้นความหนาแน่นของความน่าจะเป็นที่ปลายหางจะลดลงและการกระจายรอบๆค่ากลางจะรวมกันแน่นมาก กราฟด้านล่างแสดงการแจกแจงของ t-distribution ที่มีค่า DF เท่ากับ 5 และ 30
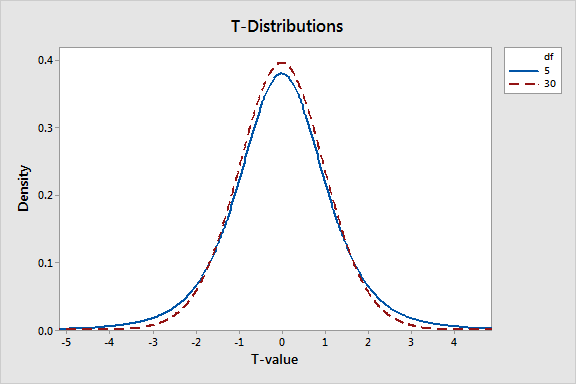
การแจกแจงค่า t-distribution ที่มีองศาอิสระน้อยกว่าจะมีหางที่หนากว่า สิ่งนี้เกิดขึ้นเนื่องจากการแจกแจงค่า t-distribution ถูกออกแบบมาเพื่อสะท้อนความไม่แน่นอนที่เพิ่มจากการวิเคราะห์ตัวอย่างขนาดเล็ก กล่าวอีกนัยหนึ่งคือถ้าคุณมีตัวอย่างขนาดเล็กความน่าจะเป็นที่ตัวสถิติของข้อมูลตัวอย่างตัวอย่างจะอยู่ห่างจากสมมติฐานหลักมากขึ้นแม้ว่าสมมติฐานหลักจะเป็นจริงก็ตาม
ตัวอย่างขนาดเล็กมีแนวโน้มที่จะเบี่ยงเบนได้มากกว่า สิ่งนี้มีผลต่อความน่าจะเป็นที่เกี่ยวข้องกับค่า t-value ที่กำหนด สำหรับ DF เท่ากับ 5 และ 30 ค่า t-value ค่า t-value เท่ากับ 2 ในการทดสอบสองด้านมีค่า p-value เท่ากับ 10.2% และ 5.4% ตามลำดับ ตัวอย่างใหญ่ดีกว่านั่นเอง!
ฉันได้แสดงให้เห็นว่าค่า t-value และการแจกแจง t-distribution ทำงานร่วมกันเพื่อได้ค่าความน่าจะเป็นได้อย่างไร หากต้องการดูว่าการทดสอบ t-test แต่ละประเภททำงานอย่างไรและจริงๆแล้วเราคำนวณค่า t-value ได้อย่างไร โปรดอ่านโพสต์ “ทำความเข้าใจการทดสอบสมมติฐาน t-Tests: 1-sample, 2-sample และ Paired t-Tests”
ถ้าต้องการเรียนรู้เกี่ยวกับ ANOVA, การทดสอบ F-test อ่านโพสต์ในหัวข้อ “Understanding Analysis of Variance(ANOVA) and the F-test”
บทความต้นฉบับ : Understanding t-Tests: t-values and t-distributions
ต้นฉบับนำมาจาก Minitab blog , แปลและเรียบเรียงโดยชลทิชา จํารัสพร
บริหารจัดการ SCM Blog โดยชลทิชา จำรัสพร, บริษัท โซลูชั่น เซ็นเตอร์ จํากัด ตัวแทน Minitab ในประเทศไทย

เพิ่มเติมเกี่ยวกับบริษัท Minitab
Minitab ช่วยให้บริษัทและองค์กรต่างๆ สามารถมองเห็นแนวโน้มของข้อมูล, แก้ปัญหาและค้นพบประเด็นสำคัญจากข้อมูลเชิงลึก โดยนำเสนอชุดโซลูชั่นที่ครอบคลุมทุกด้านและดีที่สุดสำหรับซอฟต์แวร์ในระดับเดียวกัน ที่ใช้สำหรับการวิเคราะห์ข้อมูลและการปรับปรุงกระบวนการ
ด้วยวิธีการที่เป็นเอกลักษณ์ และการนำเสนอซอฟต์แวร์และบริการแบบองค์รวม Minitab ช่วยให้องค์กรเข้าถึงกระบวนการตัดสินใจในส่วนที่ช่วยผลักดันให้เกิดความเป็นเลิศทางธุรกิจได้ดีขึ้น ความง่ายในการใช้งานที่โดดเด่นกว่าใครมีส่วนช่วยให้ Minitab สามารถทำให้การเข้าถึงข้อมูลเชิงลึกเป็นเรื่องที่ง่าย ทีมงานของ Minitab ซึ่งประกอบด้วยผู้เชี่ยวชาญทางด้านการวิเคราะห์ข้อมูลที่ได้ผ่านการอบรมมาเป็นอย่างเข้มงวด จะช่วยให้ผู้ใช้งานมั่นใจว่าจะได้รับประโยชน์สูงสุดจากการใช้งานวิเคราะห์ข้อมูลและพร้อมที่จะให้คำปรึกษาตลอดเวลาที่ใช้งานเพื่อนำไปสู่การตัดสินใจที่ดีขึ้น รวดเร็ว และแม่นยำ
เป็นเวลากว่า 50 ปีที่ Minitab ได้ช่วยองค์การต่าง ๆ เพิ่มรายได้ ควบคุมและลดต้นทุน เพิ่มคุณภาพ เสริมสร้างความพึงพอใจของลูกค้า และเพิ่มประสิทธิภาพ ธุรกิจและองค์นับหมื่นทั่วโลกใช้ Minitab Statistical Software®, Companion by Minitab®, Minitab Workspace®, Salford Predictive Modeler® and Quality Trainer® เป็นเครื่องมือช่วยในการค้นพบและปรับปรุงความบกพร่องในกระบวนการ


