“เราไม่ใช่ผู้สร้างประวัติศาสตร์ เราถูกสร้างขึ้นโดยประวัติศาสตร์” – มาร์ติน ลูเธอร์ คิง จูเนียร์
การวิเคราะห์อนุกรมเวลา (Time series analysis) มีลักษณะเช่นเดียวกับคําพูดประโยคข้างต้น คือ การให้ความสําคัญกับประวัติศาสตร์หรือในที่นี้ คือ มุ่งเน้นที่ข้อมูลที่เกิดขึ้นมาในอดีต เพื่อให้การวิเคราะห์อนุกรมเวลาได้ดีขึ้น จะต้องมีการทำความเข้าใจกับข้อมูลและ บริบทของข้อมูลเหล่านั้นอย่างละเอียด
มีข้อสังเกตบางประการเกี่ยวกับการวิเคราะห์อนุกรมเวลาที่ควรทราบ
- ข้อมูลอนุกรมเวลาทุกชุดไม่มีความจำเป็นต้องเหมือนกัน
- อย่าใช้ข้อมูลชุดย่อยเพียงหนึ่งชุดเพื่อนำไปการคาดการณ์เรื่องในอนาคตที่อยู่ไกลเกินไป
- ควรมีการปรับปรุงข้อมูลให้ใหม่อยู่เสมอเมื่อเวลาเปลี่ยนไป
ประเภทของการวิเคราะห์อนุกรมเวลา
การวิเคราะห์อนุกรมเวลาด้วยโปรแกรม Minitab Statistical Software มี 3 แบบ และแต่ละแบบมีหลักการสำคัญที่ต่างกันเพื่อให้นักวิเคราะห์สามารถเลือกใช้ได้อย่างเหมาะสม โดยจำแนกเป็นดังนี้
- แนวโน้ม (trend) หมายถึง ทิศทางของข้อมูล แนวโน้มสามารถเป็นเส้นตรงหรือกําลังสอง
- ฤดูกาล (season) หมายถึง การที่ข้อมูลเกิดวนซ้ำตามระยะเวลา
- แบบสุ่ม (random) หมายถึง ไม่มีรูปแบบของการเกิดข้อมูลที่มีชัดเจนในรูปแบบใดรูปแบบหนึ่ง
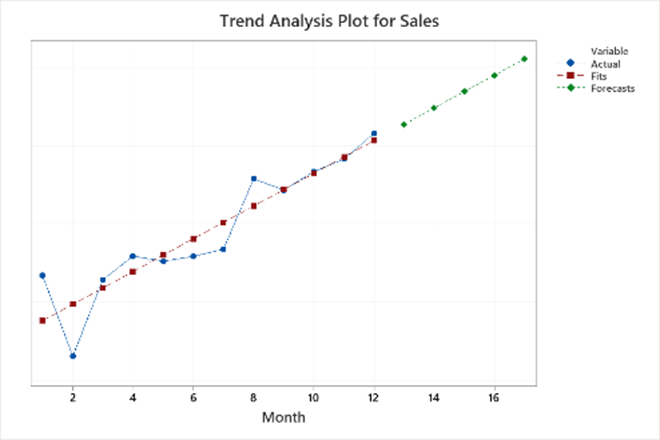
รูปด้านบนแสดงห็เห็นรูปแบบแนวโน้มที่เพิ่มขึ้นอย่างชัดเจน แต่ไม่มีรูปแบบตามฤดูกาล หรือ รูปแบบอื่นใด รูปแบบแนวโน้มสามารถเป็นได้ทั้งแบบเชิงเส้น (linear) กําลังสอง (quadratic) เอกซ์โปเนนเชียล (exponential) หรือ เส้นโค้งเอส (S) จากที่แสดงในภาพด้านบน ข้อมูลน่าจะมีรูปแบบแนวโน้มที่เป็นเส้นตรง โดยตัวแบบจะพยายามหาตัวแบบที่มีความเรียบง่ายที่สุดในการนำมาอธิบายข้อมูล
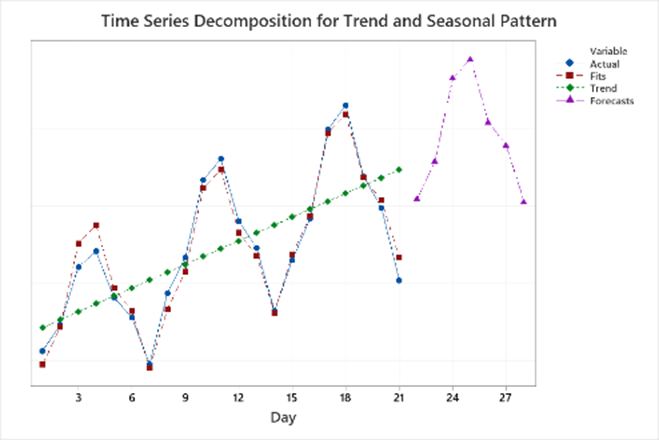
ส่วนข้อมูลชุดนี้แสดงรูปแบบที่มีแนวโน้มและรูปแบบตามฤดูกาล โดยรูปแบบตามฤดูกาลมีลักษณะว่าจะเพิ่มขึ้นตามระยะเวลาที่เปลี่ยนไป โดยมีจุดสังเกตคือระยะห่างระหว่างข้อมูล 2 จุด มีความกว้างเพิ่มขึ้น ความกว้างของระยะห่างระหว่างข้อมูล 2 จุด อาจมาจากรูปแบบที่มีความหลายหลาก หากรูปแบบตามฤดูกาลมีลักษณะคงที่ อาจจะได้ตัวแบบจําลองที่ให้ผลดีกว่านี้
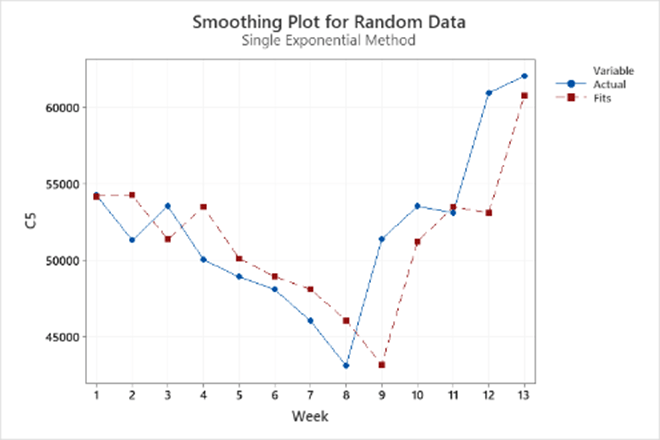
ส่วนข้อมูลชุดนี้ แสดงรูปแบบที่ไม่มีแนวโน้มหรือรูปแบบตามฤดูกาลที่เห็นได้อย่างชัดเจนจึงน่าจะเป็นรูปแบบสุ่ม ซึ่งถือเป็นเรื่องยากมากที่จะสมมติให้ตัวแบบที่มีความเป็นระบบ (systematic) มาใช้คาดการณ์สิ่งที่จะเกิดขึ้น โดยใช้ข้อมูลในอดีตที่มาจากข้อมูลที่มีลักษณะรูปแบบเช่นในภาพนี้
ในโปรแกรม Minitab มีเครื่องมือเฉพาะทาง ที่สามารถช่วยให้ผู้ใช้งานนำไปคาดการณ์กับข้อมูลที่มีรูปแบบตามประเภทที่จำแนกไว้ข้างต้น
- เมื่อข้อมูลมีรูปแบบแนวโน้มเพียงอย่างเดียว เครื่องมือที่ใช้ได้ คือ วิธีวิเคราะห์แนวโน้ม (Trend Analysis) และ วิธีปรับเรียบด้วยเอกซ์แบบเนนเชียลซ้ำ 2 ครั้ง (Double Exponential Smoothing)
- เมื่อข้อมูลมีรูปแบบแนวโน้มและฤดูกาลร่วมด้วย เครื่องมือที่ใช้ได้ คือ วิธีแยกส่วนประกอบ (Decomposition) และ วิธีของวินเธอร์ (Winter’s Method)
- เมื่อข้อมูลมีรูปแบบสุ่ม เครื่องมือที่ใช้ได้ คือ วิธีการปรับเรียบแบบด้วยเอกซ์แบบเนนเชียล (Single Exponential Smoothing) และ วิธีค่าเฉลี่ยเคลื่อนที่ (Moving Average)
ในการประเมินความเหมาะสมของตัวแบบจําลองเราจะต้องตรวจสอบความถูกต้อง (accuracy) ของการวัด: โดยตัววัดที่จะใช้ คือ เปอร์เซ็นต์ค่าเฉลี่ยความแม่นยําของข้อผิดพลาด (mean accuracy percentage of error – MAPE), ค่าเบี่ยงเบนสัมบูรณ์เฉลี่ย (mean absolute deviation – MAD) และค่าเบี่ยงเบนกําลังสองเฉลี่ย (mean squared deviation – MSD) เมื่อตัวแบบมีความเหมาะสมมากเท่าไหร่ค่าเหล่านี้ก็จะยิ่งต่ำลงเท่านั้น ค่าตัวเลขเหล่านี้โดดๆจะไม่มีประโยชน์ใดใดเลย เว้นแต่จะใช้นำไปวิเคราะห์ความสัมพันธ์กับตัวแบบอื่น ๆ
ด้านล่างนี้เป็นตัวอย่างของการวิเคราะห์แนวโน้มด้วยตัวแบบแบบที่มีการเติบโตในลักษณะกําลังสองและเอกซ์โปเนเชียล เพื่อใช้ทํานายจํานวนเซลล์ที่เติบโตเมื่อเวลาผ่านไป สําหรับการทดลองทางเภสัชกรรมในการปลูกเนื้อเยื่อใหม่สําหรับรากฟันเทียม

เมื่อดูที่ค่าวัดความถูกต้องของตัวแบบจําลองแบบเอกซ์โปเนนเชียลให้ผลลัพธ์ที่ดีกว่า นั่นหมายความว่าตัวแบบที่มีความถูกต้องมากกว่าน่าจะให้ผลของการคาดการณ์ได้ดีกว่า การใช้ตัวแบบที่มีความเหมาะสมกว่าทำให้นักวิเคราะห์สามารถคาดการณ์ได้ว่าเมื่อใดคือเวลาที่มีจำนวนเซลล์ที่เติบโตจนเพียงพอที่จะทำให้รากฟันเทียมนั้นพร้อมนำไปใช้งาน
การคาดการณ์ที่เสมือนจริง
เป้าหมายของการวิเคราะห์อนุกรมเวลาใด ๆ คือ การคาดการณ์สําหรับการตัดสินใจทางธุรกิจให้ใกล้เคียงกับความเป็นจริง และในการคาดการณ์ที่มีระยะเวลาที่ไกลเกินไปจะทำให้การคาดการณ์นั้นอาจมีข้อผิดพลาดมากขึ้น ในตัวอย่างต่อไปจะแสดงให้เห็นถึงการใช้ข้อมูลที่เก็บมาได้ 14 ค่า และนำไปใช้คาดการณ์ข้อมูล จำนวน14 ครั้งล่าสุด
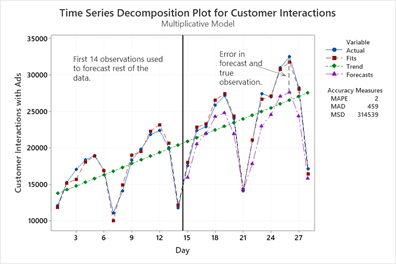
จากตัวแบบที่เลือกมาแสดงนี้ มีผลลัพธ์การคาดการณ์ที่ดูเหมือนว่าจะมีความเหมาะสมดี ซึ่งเห็นได้จากค่าที่คาดการณ์ไว้มีความใกล้เคียงกับข้อมูลที่เกิดขึ้นจริง แต่เนื่องจากเราใช้จุดข้อมูลเพียง 14 จุดเพื่อทํานายข้อมูลอีก 14 จุดล่าสุดนับจากท้าย จึงทำให้เกิดความคลาดเคลื่อนเพิ่มขึ้นเรื่อยๆเมื่อเวลาที่ไกลออกไป ดังนั้นจึงควรหลีกเลี่ยงการพยากรณ์ที่มีระยะเวลาที่ไกลเกินไป การวิเคราะห์อนุกรมเวลามีความเปลี่ยนแปลงตลอดเวลาจึงควรมีการปรับเปลี่ยนข้อมูลให้ทันสมัยอยู่เสมอ
การวิเคราะห์อนุกรมเวลามีความไม่คงที่
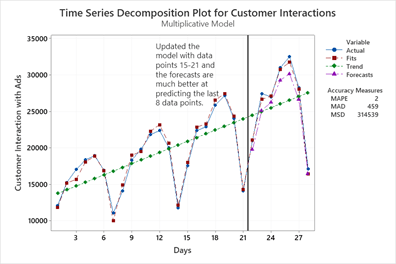
ตัวแบบที่ใช้ในการคาดการณ์จะยิ่งมีประสิทธิภาพในการใช้งานมากขึ้นเมื่อมีการปรับชุดข้อมูลในการสร้างตัวแบบจำลองอย่างสม่ำเสมอ ถ้าใช้กราฟที่แสดงในภาพด้านบนเป็นตัวอย่าง เมื่อเราทำการเพิ่มจำนวนจุดข้อมูลอีก 7 จุด (คือ ข้อมูลในวันที่ 15 – 21) ทำให้เราได้กราฟที่เปลี่ยนไปในภาพด้านล่าง จะเห็นได้ว่าในภาพกราฟด้านบนมีความคลาดเคลื่อนขนาดใหญ่ในในวันที่ 26 แต่เมื่อมีการเพิ่มข้อมูลใหม่เข้าไปในตัวแบบ ทำให้การคาดการณ์ของเรามีความใกล้เคียงกับความจริงมากยิ่งขึ้น
สรุป
ตัวแบบที่ใช้ในการวิเคราะห์อนุกรมเวลาต้องมีการใช้วิธีการหลากหลายๆแบบในการสร้างตัวแบบ และยังต้องมีการเปรียบเทียบตัวแบบจําลองที่แตกต่างกันนั้นด้วยเพื่อหาตัวแบบที่เหมาะสมที่สุด ด้วยการตรวจสอบความถูกต้องของการวัดเพื่อดูว่าตัวแบบใดมีความคลาดเคลื่อนน้อยที่สุด นอกจากนี้ก่อนใช้ตัวแบบเพื่อการคาดการณ์ควรจะมีการทวนสอบด้วยว่าตัวแบบนั้นใช้งานได้เหมาะสมกับข้อมูลได้ดีจริงๆ
บทความต้นฉบับ : An Introduction to Time Series Analysis in Minitab Statistical Software
ต้นฉบับนำมาจาก Minitab blog, แปลและเรียบเรียงโดยสุวดี นำพาเจริญ,
บริหารจัดการ SCM Blog โดยชลทิชา จำรัสพร บริษัท โซลูชั่น เซ็นเตอร์ จํากัด ตัวแทน Minitab ในประเทศไทย

เพิ่มเติมเกี่ยวกับบริษัท Minitab
Minitab ช่วยให้บริษัทและองค์กรต่างๆ สามารถมองเห็นแนวโน้มของข้อมูล, แก้ปัญหาและค้นพบประเด็นสำคัญจากข้อมูลเชิงลึก โดยนำเสนอชุดโซลูชั่นที่ครอบคลุมทุกด้านและดีที่สุดสำหรับซอฟต์แวร์ในระดับเดียวกัน ที่ใช้สำหรับการวิเคราะห์ข้อมูลและการปรับปรุงกระบวนการ
ด้วยวิธีการที่เป็นเอกลักษณ์ และการนำเสนอซอฟต์แวร์และบริการแบบองค์รวม Minitab ช่วยให้องค์กรเข้าถึงกระบวนการตัดสินใจในส่วนที่ช่วยผลักดันให้เกิดความเป็นเลิศทางธุรกิจได้ดีขึ้น ความง่ายในการใช้งานที่โดดเด่นกว่าใครมีส่วนช่วยให้ Minitab สามารถทำให้การเข้าถึงข้อมูลเชิงลึกเป็นเรื่องที่ง่าย ทีมงานของ Minitab ซึ่งประกอบด้วยผู้เชี่ยวชาญทางด้านการวิเคราะห์ข้อมูลที่ได้ผ่านการอบรมมาเป็นอย่างเข้มงวด จะช่วยให้ผู้ใช้งานมั่นใจว่าจะได้รับประโยชน์สูงสุดจากการใช้งานวิเคราะห์ข้อมูลและพร้อมที่จะให้คำปรึกษาตลอดเวลาที่ใช้งานเพื่อนำไปสู่การตัดสินใจที่ดีขึ้น รวดเร็ว และแม่นยำ
เป็นเวลากว่า 50 ปีที่ Minitab ได้ช่วยองค์การต่าง ๆ เพิ่มรายได้ ควบคุมและลดต้นทุน เพิ่มคุณภาพ เสริมสร้างความพึงพอใจของลูกค้า และเพิ่มประสิทธิภาพ ธุรกิจและองค์นับหมื่นทั่วโลกใช้ Minitab Statistical Software®, Companion by Minitab®, Minitab Workspace®, Salford Predictive Modeler® and Quality Trainer® เป็นเครื่องมือช่วยในการค้นพบและปรับปรุงความบกพร่องในกระบวนการ